A reductio ad absurdum argument in defense of those “incredible” age numbers in Genesis 5 and 11

by Richard Peachey

** Warning to readers! This article contains Mathematics. Proceed at your own risk! **

Abstract

The genealogies in Genesis 5 and 11 report ages that many readers find difficult to take at face value since the numbers do not match our own experience. The various explanations that have been offered for these numbers tend to assume that the Genesis author(s) “contrived,” “invented,” and “fabricated” them, using some mathematical and/or astronomical scheme. Combinations of 60s and 7s, algebraic equations, sums of squares and products, lists of factors, and other intriguing patterns have been suggested to account for these “incredible,” “excessively large” numbers. This article defends the Genesis numbers by showing that similar patterns and statistical improbabilities are found among the ages of the ten British monarchs beginning with George I. Accordingly, if the Genesis genealogies are judged as fabrications on the basis of their mathematical features, logical consistency dictates that the British monarchy must likewise be relegated to the realm of fiction!

Introduction

Readers of Genesis have long puzzled over the “excessively large” [1] lifespans listed in Genesis chapters 5 and 11. Since the reported ages at death lie far beyond our current experience, the numbers are often assumed to be either false or symbolic. Explanations are then sought for the intellectual process(es) of the author(s) who produced these numbers. As scholars formulate their hypotheses they search for, and claim to discover, mathematical patterns among the data.

In a 2003 article, Carol A. Hill wrote:

All age-numbers (30 in all) from Adam to Noah are a combination of the sacred numbers 60 (years and months) and 7. No numbers end in 1, 3, 4, 6, or 8—a chance probability of one in a billion. Thirteen numbers end in 0 (some multiple or combination of 60), 8 numbers end in 5 (5 years = 60 months), 3 numbers end in 7, 5 numbers end in 2 (5yrs + 7yrs = 12), and 1 number ends in 9 (5yrs + 7yrs + 7yrs = 19). All of this cannot be coincidental. The Mesopotamians were using sacred numbers, not real numbers. Therefore, these numbers were not meant to be (and should not be) interpreted as real numbers. [2]

Hill’s table of patriarchal ages and their Mesopotamian representations is shown as Figure 1 below.

 

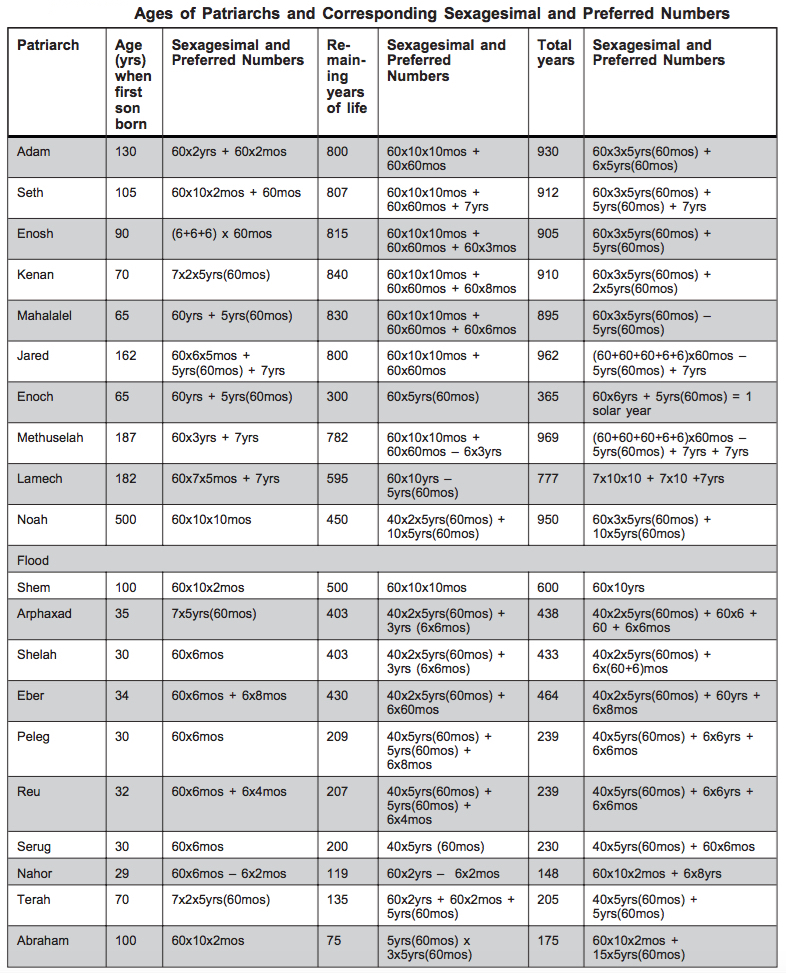
Figure 1. Carol A. Hill’s table of patriarchal ages and their Mesopotamian representations. [3]

 

Based on (a) the convertibility of the age numbers into combinations of 60s and 7s, and (b) the statistical unlikelihood of the occurrences of the final digits of the age numbers, Hill argues that the numbers should not be understood as “real” (i.e., historical). Following (for the most part) Umberto Cassuto’s commentaries on Genesis [4], she splits each age value into components involving 60, the number at the core of the Mesopotamian sexagesimal system, and 7, a number with special meaning throughout the Bible but particularly in Genesis. In Hill’s view, the mathematical patterns and improbabilities observed in the genealogies point to “the fact that the numbers in Genesis may have been ‘contrived’ or ‘intentional’ rather than ‘real'” [5] and thus they should be interpreted “figuratively” [6].

In a later letter to the editor, Hill again emphasized her argument from improbability, at the same time indicating one common motivation for questioning the reality of the age numbers:

Surely, if all of the ages listed in Table 2 of my Numbers article are statistically random numbers, as should be expected for real ages, such numerical improbabilities would not exist. . . . Thus, these ages cannot be used to construct a 6,000-year-old universe or planet Earth. [7]

Below are some further examples of statements made by scholars regarding the “invented” [8], “incredible” [9], suspiciously patterned and improbable numbers of Genesis 5 and 11:

• Kenton L. Sparks:

If we look closely at the chronological figures in Gen 5, we’ll find that these are certainly symbolic rather than literal. The final digit for each number is 0, 2, 5, or 7 in all cases but one. Given that the probability of random ages like this is on the order of .00000006%, it is clear that these numbers are not chronological in the usual sense. A comparison of these numbers with the ancient Near Eastern evidence suggests that in both cases—the biblical and Mesopotamian king lists—the numbers were derived from, or influenced by, astronomical and mathematical figures. So it has always been a mistake to use the lifespans in Genesis to reconstruct actual human history, as Archbishop Ussher once tried to do, and many continue to do. [10]

• Dwight Wayne Young:

The settling of Noah’s total years is an excellent example: 625 + 225 + 100 = 950 [i.e., 25² + 15² + 10² = 950, and note, 25 = 15 + 10]. When ascribing great longevity with such numbers, the author, if many hours spent at mastering the basic curriculum in algebra had accrued to him, was doing nothing unusual or bizarre; he was merely utilizing what he understood best. . . .

The author of the incredible biblical lifetimes was familiar with at least the basic algebraic equations taught in Babylonian schools and used the numerical relationships displayed in them to construct his scheme. He drew upon the most important numerical group in Babylonian algebra, which has as its core the numbers 30 and 20 and the difference between them [i.e., 30 – 20 = 10]. The group includes principally their squares (100, 400, 900) and 600, the product  of the two primary numbers [i.e., 30 x 20 = 600]. Another closely related number is 800, which arises in the simplest of the Babylonian quadratic equation problems that has come down to us by multiplying   30 + (30 – 20) by 20 [i.e., 40 x 20 = 800]. [11]

• Donald V. Etz:

The general objective of the author [in Genesis 5] was apparently to provide “larger than life” numbers that would emphasize the superiority of the revered ancestors of the Hebrew people by demonstrating their superior longevity. . . . For the other list, from Shem to Terah (Gen. xi 10-26), the author apparently constructed a linear genealogy resembling that of Gen. v, and invented numbers for it. [12]

Response to the scholars: A reductio ad absurdum argument using the British Monarchy

One possible response to statements like the foregoing is a reductio ad absurdum argument. If the logic of Hill and others were correct, it would prove too much. It would relegate not only the biblical patriarchs but also the British monarchs to the dustbin of contrived fiction. (Here I am using the term “patriarch” to refer to any man in the direct genealogical line from Adam to Abraham.)

In this article I will focus on the ages at death of the first ten patriarchs in comparison to those of the ten British monarchs beginning with George I, whom I will designate as “The Ten British Monarchs” [13]. Refer to Table 1 below. (Anne, who preceded George I, was actually also a “British” monarch — in the sense of ruling “Great Britain” — but only for part of her reign; and her genealogical relationship to George I and his successors was rather distant [14].)

Note that Enoch’s number is in parentheses because, as made clear by Hebrews 11:5, he did not actually die.

 

The First Ten Patriarchs	Age at Death	The Ten British Monarchs	Age at Death
Adam	930	George I	67
Seth	912	George II	76
Enosh	905	George III	81
Kenan	910	George IV	67
Mahalalel	895	William IV	71
Jared	962	Victoria	81
Enoch	(365)	Edward VII	68
Methuselah	969	George V	70
Lamech	777	Edward VIII	77
Noah	950	George VI	56

 

Table 1. Longevities of the first ten biblical patriarchs and the ten British monarchs. [15]

Observations

1. (a) The final digits of the patriarchs’ ages are all elements of the set {0, 2, 5, 7, 9}. (Or, as pointed out by Hill [16], there are no final digits from the set {1, 3, 4, 6, 8}.)
    (b) The final digits of the monarchs’ ages are all elements of the set {0, 1, 6, 7, 8}.
    Conclusion: The probabilities of these two observations, however one may decide to calculate them, are exactly equal.

2. (a) The non-zero numbers in the patriarchs’ set of final digits (see #1) are all related to one another through simple addition, i.e., 2 + 5 = 7, and 2 + 7 = 9. This seems suspicious.
    (b) The non-zero numbers in the monarchs’ set of final digits are, similarly, all related to one another through simple addition: 1 + 6 = 7, and 1 + 7 = 8. This would be equally suspicious.
    Conclusion: Here the two lists are on equal footing. In both cases, the set’s second digit plus its third digit equals its fourth digit, while the second digit added to the fourth digit equals the fifth digit.

3. (a) There are two patriarchal ages containing a final digit that is only used once: Methuselah (‘9’) and Lamech (‘7’). These two men were father and son.
    (b) There are two monarchal ages containing a final digit that is only used once: Edward VII (‘8’) and George V (‘0’). These two men were also father and son.
    Conclusion: Once again, the two lists are on equal footing in regard to this feature.

4. (a) If Methuselah and Lamech are removed from the patriarchal list, the remaining final digits are all elements of the set {0, 2, 5}. Using the reduced set, there are in the list three instances of the first digit, two of the second digit, and three of the last digit.
    (b) If Edward VII and George V are removed from the monarchal list, the remaining final digits are all elements of the set {1, 6, 7}. Using the reduced set, there are in the list three instances of the first digit, two of the second digit, and three of the last digit. As well, note that 1 + 6 = 7.
    Conclusion: The two lists are remarkably equal in this aspect, except for the additional curiosity that the digits in the monarchal set can be written into a simple equation.

Having considered several aspects of statistical probability related to these two lists, it is now clear that, to use Hill’s words [17], “all of this cannot be coincidental.” Clearly, the author(s) of the list of British monarchs were “using sacred numbers, not real numbers.” That is to say, on the points considered so far, it is equally true for the monarchs as for the patriarchs that “these numbers were not meant to be (and should not be) interpreted as real numbers”(!) Alternatively, if one takes the realistic position that these probability considerations are not sufficient to turn the monarchal list into fiction, one ought to be logically consistent and apply the same leniency to the patriarchal list.

By the way, it’s worth noting that when compared to the longevities for the second patriarchal list (Shem to Abraham, Genesis 11:10-32; 25:7), the ages in the monarchal list look even more contrived. The final digits of these patriarchal ages are all elements of a set of six numbers, {0, 3, 4, 5, 8, 9}, whereas those of the monarchs are from a more constrained set of only five. (See Figure 1, Hill’s table.) Again, in the second patriarchal list no final digit occurs more than twice, but in the monarchal list there are two triplets (three each of 1 and 7). Furthermore, in the second patriarchal list only two of the ages are exactly the same (239 for both Peleg and Reu), while among the monarchs there are two pairs of identical ages.

Justification for comparing patriarchs with monarchs

Are these two lists really comparable? I suggest they are, for the following reasons:

1. Both lists name ten individuals who have died (except Enoch), with their ages at death.
2. Both lists involve close genealogical relationships.

The patriarchal list from Adam to Noah is presented as a direct line of father-son relationships. There is no clear textual evidence of between-generation gaps. The fact that three age numbers are given for each man distinguishes this genealogy from others where gaps may arguably be present. Certainly in cases where one man names another—such as Adam naming Seth (Genesis 5:3), Seth naming Enosh (Genesis 4:26), and Lamech naming Noah (Genesis 5:29)—the presumption must be in favour of an immediate genealogical relationship.

The monarchal list is not quite as tightly genealogical, yet each monarch is closely related to the previous one [18]. Refer to Table 2 below.

 

The Ten British Monarchs	Relationship to Predecessor	Reason for Accession to the Throne (if not son or daughter)
George I
George II	son
George III	grandson	George III’s father Frederick predeceased George II
George IV	son
William IV	brother (George III’s son)	George IV had no surviving children
Victoria	niece (George III’s granddaughter)	Neither William IV nor George III had surviving legitimate children
Edward VII	son
George V	son
Edward VIII	son
George VI	brother (George V’s son)	George VI became king when Edward VIII abdicated

 

Table 2. Genealogical relationships among the ten British monarchs.

Mathematical Patterns

Having already established, based on a study of the final digits, that the patriarchal longevities from Adam to Noah are at least as statistically probable as those of the British monarchs, let us now investigate possible mathematical patterns among the monarchal numbers.

A. Between-age connections among the monarchal ages

As one proceeds down the list of the monarchal ages, each number seems to be related to the previous one (or more) via repetition, addition and/or subtraction. (Only William IV’s age of 71 is left unexplained at this point.) Refer to Table 3 below.

 

The Ten British Monarchs	Age at Death	Between-age Connections Among the Monarchal Ages
George I	67
George II	76	= first number reversed!
George III	81	= difference between the first two numbers, multiplied by itself!
George IV	67	= first number, repeated!
William IV	71
Victoria	81	= third number, repeated! (And again, ’81’ appears as the second number following ’67.’)
Edward VII	68	= 67 – 76 + 81 + 67 – 71 (addition/subtraction using the first five numbers)
George V	70	= 81+ 67 + 71 – 81 – 68 (addition/subtraction using the last five numbers)
Edward VIII	77	= 67 – 71 + 81 (addition/subtraction using the middle three numbers to this point)
George VI	56	= 67 – 76 + 81 – 67 + 71 – 81 + 68 +70 –77 (addition/subtraction using all previous numbers)

 

Table 3. Mathematical connections among the ages of the first ten British monarchs.

Observations

1. (a) In the patriarchal list, no number is repeated.
    (b) In the monarchal list, two numbers are repeated, with the same spacing between them (’81’ occurs as the second number following ’67,’ both times). Also, both times there is a number beginning with ‘7’ between them, so that the first digits of the first six numbers can be read as “6, 7, 8, 6, 7, 8.”
    Conclusion: This all seems quite artificial. On this point, suspicion of possible fabrication in the monarchal list is certainly warranted more than it would be for the patriarchal list. (The appearance of ’81,’ a power of 3, in both the third and sixth rows seems designed to signal the reader to be on the watch for patterns involving “every third row.” By the time we reach Table 9, this quiet signal will have become an overwhelming roar!)

2. (a) For the patriarchal list, I have not seen any scholar suggest that the last four numbers can be generated by addition/subtraction of the earlier numbers.
    (b) For the monarchal list, each of the last four numbers can be generated using an intriguing pattern of addition/subtraction of earlier numbers. The seventh number is formed from the first five numbers; the eighth from the last five numbers to that point; the ninth from the middle three numbers to that point; and the last from all of the previous numbers!
    Conclusion: Supporting evidence for invention of numbers appears to be stronger here for the monarchal list than it is for the patriarchal list.

B. The pattern of between-age differences among the monarchs

Differences between the first and last age numbers, the second and second-last numbers, etc., exhibit a curious pattern, as shown in Table 4.

 

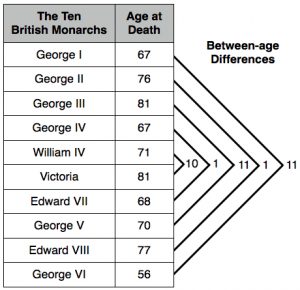
Table 4. Between-age differences for the ten British monarchs.

Observations

1. (a) For the patriarchal list, I am not aware of any scholarly suggestion that the differences between matched numbers form any sort of pattern.
    (b) In the monarchal list, the differences between the paired numbers (first with last, second with second-last, etc.) form a distinct pattern, which can be read as: “10 is 1 from 11, yes, 1 from 11” (i.e., starting from the middle, the fourth and fifth differences are repetitions of the second and third differences, respectively).
    Conclusion: This is a fascinating result. Either it is a wonderful coincidence, or it is evidence of a carefully designed pattern in the monarchal list. This specific sort of either/or quandary does not face us in connection with the patriarchal list.

2. If the differences are allowed to retain their signs (positive or negative) when each subtraction is performed (top to bottom), the results are as follows: –10, –1, +11, –1, +11. The addition of these numbers produces 10, the number of the monarchs in the list!
    Conclusion: Each small piece of evidence of this sort continues to contribute to an overall sense of artifice rather than expected randomness among the monarchal numbers.

3. Up to this point we had been at a loss to explain the fifth number, ’71,’ which, unlike the fourth and sixth numbers, was not a repetition of one of the first three. But we can now see that this number, like all the rest, fits into a clear pattern.
    Conclusion: This realization adds further strength to the mounting evidence that the age numbers connected to the British monarchy were contrived, invented, and fabricated(!)

C. The Mesopotamian connection: 60s and 7s among the monarchal numbers

As has been noted above, Hill, Cassuto, and others have suggested that the patriarchal numbers were invented by arranging combinations of 60s and 7s. Could this also be the case with the monarchal numbers? Refer to Table 5 below.

 

The Ten British Monarchs	Age at Death	Mesopotamian Formulation (using 60s and 7s)
George I	67	= 60 + 7 (obviously Mesopotamian!)
George II	76	= 60 + 3 x 7 – 60months
George III	81	= 60 + 3 x 7
George IV	67	= 60 + 7 (again!)
William IV	71	= 60 + 3 x 7 – 2 x 60months
Victoria	81	= 60 + 3 x 7 (again!)
Edward VII	68	= 60 – 7 + 3 x 60months
George V	70	= 60 + 2 x 60months
Edward VIII	77	= 60 + 7 + 2 x 60months
George VI	56	= 60 – 2 x 7 + 2 x 60months

 

Table 5. Ages of the ten British monarchs resolved into components of 60s and 7s.

Observations

1. (a) In Hill’s table (see Figure 1), none of the patriarchal ages is composed of a simple ’60,’ which is the fundamental unit of the Mesopotamian sexagesimal system (or even a simple ‘360’ or ‘600’). Six of the ages begin with “60x3x5yrs;” a further two begin with “(60+60+6+6+6)x60mos.” These complicated numbers have clearly taken some ingenuity to work out. (This is not to say that the Genesis numbers themselves look fabricated, but rather that Hill’s formulations seem contrived.)
    (b) Each monarchal age-formulation is based on a single ’60,’ and every age is within 21 (= 3 x 7) years of 60.
    Conclusion: The monarchal ages are much simpler to base on ’60,’ and the overall expressions appear a lot less complicated (therefore less “forced”), than Hill’s patriarchal formulations.

2. (a) Hill’s formulations of the patriarchal ages incorporate adjustments of one, two, six, or ten units of 5 years (= 60 months).
    (b) The monarchal ages require adjustment by zero, one, two, or three units of 5 years to be expressed as Mesopotamian-style numbers.
    Conclusion: The monarchal numbers, since they require less adjustment of this kind than do the patriarchal numbers, appear more credible as examples of Mesopotamian influence. Accordingly, the monarchal numbers seem more likely to have been “contrived” along such lines than do the patriarchal numbers.

3. (a) Hill’s Mesopotamian-style formulations of the patriarchal ages incorporate adjustment by zero, one, or two units of 7 years.
    (b) To be expressed as Mesopotamian-style numbers, the monarchal ages require adjustment by zero, one, two, or three units of 7 years.
    Conclusion: By this criterion on its own, the patriarchal ages admittedly fit better into a Mesopotamian pattern than do the monarchal numbers.

4. (a) Hill makes no attempt to explain Lamech’s age of 777 as a sexagesimal number.
    (b) The monarchal numbers (including Edward VIII’s ’77’) are all readily expressed as sexagesimal numbers (’60’ with adjustments as displayed above).
    Conclusion: The monarchal numbers fit more fully into a Mesopotamian numerical scheme than do the patriarchal numbers. Recall that according to Hill, “The Mesopotamians were using sacred numbers, not real numbers. Therefore, these numbers were not meant to be (and should not be) interpreted as real numbers.” [19] In that case, the British monarchy seems even more likely than the Genesis 5 genealogy to be based on “sacred” rather than “real” numbers—especially when we note the appearance of a number like “60 + 7” in the very first row of the table, and repeated three rows later!

It should be noted that in the second part of her table (dealing with the genealogy from Shem to Abraham) Hill’s sexagesimal formulations start to fail her. (Refer to Figure 1, Hill’s table.) She is forced to adjust her numbers by such quantities as “6x2mos” (Nahor), “6x4mos” (Reu), “6x6mos” (Arphaxad, Shelah, Peleg, Reu), and “6x8mos” (Eber, Peleg). These quantities, interpreted, are 1 year, 2 years, 3 years, and 4 years. Along with the adjustments of 5 years and 7 years that she has already allowed herself, there is now nothing to prevent her from generating any whole number desired. (P. G. Nelson has already called attention to this flaw in her table [20]; and Hill’s response to Nelson [21] did not adequately address this issue.) Accordingly, Hill’s “Mesopotamian” formulations do not provide as strong support for her view as she might have hoped. (Note that Cassuto himself, whom Hill was generally following, did not recommend such adjustments; he instead preferred other expedients [22]. Hill understandably opted not to follow Cassuto at this point, but her tactics in dealing with the [for her] problematic numbers in the Genesis 11 genealogy have their own drawbacks.)

D. The influence of Babylonian algebra: equations involving squares and products

Having studied the sorts of math problems used in Babylonian schools, D. W. Young believes he can explain the invention of such age numbers as Adam’s 930 and Noah’s 950.

It requires no stretch of the imagination to allow that the author of the biblical life spans, if he was trained in Babylonian mathematics, latched on to this so-called Arabic type of equation, x.² + ax = b, to establish the length of lifetime for the first man, Adam. Reaping the benefit of such a basic type of algebraic equation is a fitting manner indeed in which to inaugurate a series of figures given as the number of years lived by the biblical patriarchs. As we have seen, the given numbers in the relevant problem are [a =] 1 and [b =] 930 [with the solution of x = 30 yielding the equation 30² + 1 x 30 = 930]. [23]

A chronologist drawing upon the resources of Babylonian algebra would have found 950 to be an appropriate number for his scheme, since it is the sum of three squares whose roots are multiples of five. Multiples of five from 10 to 30 occur frequently in Babylonian sexagesimal operations because they facilitate the attainment of positive solutions. The squares of such numbers that yield a sum of 950 are 625, 225 and 100. The root of the smallest square is in fact the difference between the roots of the other squares: 25 – 15 = 10. Therefore, a mathematician can arrive at an equation with three squares by positing initially only two squares, as though he were squaring the sides of a rectangle: x.² + y.² + (x – y )² = 950. This proposition affords a most attractive mathematical explanation for Noah’s term of life. [24]

Could Babylonian-style algebra, with its enjoyment of mathematical squares, products, and sums thereof, have also influenced the British monarchal numbers? Refer to Table 6 below.

 

The Ten British Monarchs	Age at Death	Babylonian Formulation (sums of squares and/or products)
George I	67	= 52 + 6 x 7
George II	76	= 32 + 52 + 7 x 6
George III	81	= (8 + 1)2
George IV	67	= 52 + 6 x 7
William IV	71	= 82 + 7 x 1
Victoria	81	= (8 + 1)2
Edward VII	68	= 22 + 42 + 6 x 8
George V	70	= 2 x 5 x (7 + 0) [Note: 2 + 5 = 7.] Or: 70 = 52 + 72 – 22 [Note: 5 = 7 – 2.]
Edward VIII	77	= 82 – 62 + 7 x 7
George VI	56	= 4 x 5 + 62 Or: 56 = 72 + 7 [just like Adam’s 930 = 302 + 30] Or: 56 = 62 + 42 + 22, where 6 – 4 = 2 [just like Noah’s 950 = 252 + 152 + 102, where 25 – 15 = 10]

 

Table 6. Ages of the ten British monarchs displayed as sums of squares and/or products.

Observations

1. (a) For the patriarchal list, I am not aware that any scholar has produced a concise, easy-to-read table of how each of the ages could be presented as a sum of no more than three products and/or squares.
    (b) For the monarchal list, Table 6 not only shows how each age is equivalent to a simple formulation of products and/or squares (with three terms maximum), but also each digit of the age is found within the formulation, and in each case the two digits of the age are adjacent to each other in the respective formulation.
    Conclusion: Under this criterion, the current evidence is that the monarchal list appears to look more “fabricated” than does the patriarchal list. Of course, it is possible that further work by scholars may lead to new evidence in this regard.

2. (a) For the patriarchal list, D. W. Young has shown how some patriarchal ages can be construed as solutions to Babylonian-like equations. Examples include Adam’s age as a sum of a number and its square (930 = 30² + 30) and Noah’s lifespan as a sum of three squares, the roots of which form an equation of their own (950 = 25² + 15² + 10², where 25 – 15 = 10).
    (b) Such examples also occur in the monarchal list. As shown in Table 6, the ages of George V and George VI can be formulated using such patterns. In fact, George VI’s age of 56 can be formulated using the patterns discussed in Young’s calculations for the ages of both Adam and Noah! I am not aware that such a phenomenon has been demonstrated for any patriarchal number.
    Conclusion: This evidence supports the view that the monarchal numbers appear at least as “contrived” and “fabricated” as the patriarchal numbers.

3. (a) Within the patriarchal list, I am not aware that any scholar has suggested a chiasm of any sort.
    (b) Within the monarchal list, there is a beautiful six-member chiasm running from George II to Edward VII. Refer to Table 7 below. Observe that at the centre of the chiasm stand the two brothers George IV and William IV, both carrying the regnal number (i.e., Roman numeral) 4, which happens to be the only repeated regnal number in the whole monarchal list. And the difference between the brothers’ ages is, likewise, 4. And the difference between the sum of the first three ages in the chiasm, and the sum of the last three ages, is, again, 4. And the total of all the ages in this chiasm is, amazingly, 444.

 

George II	76	A     = 32 + 52 + 7 x 6
George III	81	B     = (8 + 1)2
George IV	67	C     = 52 + 6 x 7
William IV	71	C’    = 82 + 7 x 1
Victoria	81	B’    = (8 + 1)2
Edward VII	68	A’    = 22 + 42 + 6 x 8

 

Table 7. George II to Edward VII: chiasm of age numbers as squares and/or products.

4. Furthermore, the prime factors of the ages in the above chiasm also form a striking chiasm of their own, of a sort which (so far as I have been able to discover) is not seen in either of the complete lists (monarchal or patriarchal), nor within any fragment of the patriarchal list. Refer to Table 8 below.

 .

George II	76	A     = 2 x 2 x 19
George III	81	B     = 3 x 3 x 3 x 3
George IV	67	C     = 67 (prime)
William IV	71	C’    = 71 (prime)
Victoria	81	B’    = 3 x 3 x 3 x 3
Edward VII	68	A’    = 2 x 2 x 17

 

Table 8. George II to Edward VII: chiasm of prime factors of age numbers.

Conclusion: This fascinating and charming evidence engenders a strong suspicion that a brilliant mathematician may have contrived and arranged the monarchal numbers(!) The evidence for invention of the patriarchal numbers pales in comparison.

E. Orderly arrangement of ages

The monarchal ages can be ranked from 1 (for the greatest age, George III) to 10 (for the lowest age, George VI).  These rankings form a highly ordered pattern. Refer to Table 9 below.

.

The Ten British Monarchs	Age at Death	Rank in order of Longevity (1 = Greatest Age)
George I	67	9
George II	76	4
George III	81	1 (George III lived about three weeks longer than Victoria.)
George IV	67	8 (George IV lived about ten months longer than George I.)
William IV	71	5
Victoria	81	2
Edward VII	68	7
George V	70	6
Edward VIII	77	3
George VI	56	10

 

Table 9. Ages of the British monarchs ranked from greatest (1) to least (10).

Observations

1. (a) For the patriarchal list, I am not aware that any scholar has proposed (nor have I discerned) any sort of orderly arrangement of the ages at death.
    (b) For the monarchal list, Table 9 shows an astonishingly regular arrangement evidencing intention on the part of the author:

• The greatest age is found in row 3 of the list; the second greatest in row 6; and the third greatest in row 9.
• Scrolling back to the top of the list, the fourth greatest age is placed in what we can call row “12” (i.e., row 2 the second time around); the fifth greatest in row “15;” and the sixth greatest in row “18.”
• Up to this point, there has been complete consistency in handling the six greatest ages: after each age, the next greatest age always appears three rows later. If the author had continued this procedure, then, scrolling once again to the top of the list, we would anticipate finding the seventh greatest age in row “21;” the eight greatest in row “24;” the ninth greatest in row “27;” and the tenth greatest (i.e., lowest) age in row “30.” This expectation is partially, but not fully, met.
• The eighth and tenth greatest ages are found exactly where anticipated, but the seventh and ninth greatest ages have been switched with each other. What could have led to this single alteration in an otherwise perfectly consistent arrangement? One intriguing possibility is that the author was attracted by the idea of locating Edward VII (i.e., the 7th), who lived the 7th longest life, in the 7th row of the table! (This is reminiscent of the “triple 7” feature connected with both of the Lamechs in Genesis 4:24; 5:31.)

    Conclusion: The almost perfect pattern in the ranking of ages, accompanied by an attractive explanation of the lone inconsistency, constitutes powerful evidence of deliberate design in the monarchal list. No such pattern has been reported for the patriarchal list.

Three further considerations regarding the claim that the Genesis ages were fabricated

1. No math-based fabrication proposal has won general scholarly support

While setting forth his own Mesopotamian-style formulations, Cassuto dismissed the suggestions of earlier scholars:

By complicating the subject and working out a multiplicity of sums, it is possible to discover in the text whatever we wish, for the figures are flexible and can be made to fit all sorts of numerical combinations and to serve all kinds of constructions that may occur to each and every exegete. [25]

Scholars who came after Cassuto, however, have likewise dismissed his work. (And inasmuch as Hill closely follows Cassuto, a critique of Cassuto is at the same time a critique of Hill.)

After referring to E. Speiser, E. Hornung, B. Vawter, and C. Westermann, D. W. Young wrote:

It is noteworthy, however, that each of these scholars has rejected, by passing over in silence, the pseudo-mathematical view of U. Cassuto, A Commentary on the Book of Genesis I, 1972, 252–290, which was first expressed in an essay in Hebrew in . . . 1946. [26]

Before proposing his own algebra-based scheme, Etz stated:

Many arithmetic schemes have been proposed, but none has been generally accepted. They often involve complex calculations that seem unrelated to the objective, and no single scheme accounts for all the numbers. It seems reasonable to conclude that the numbers are a random set. As noted by Lloyd R. Bailey, Noah (Columbia, South Carolina, 1989), p. 124, the attempt to derive the numbers from the base 60 “leaves the vast majority of the numbers unexplained”, and equating 60 months with 5 years does not “solve the mystery of the specific ages”. [27]

Richard Johnson has supplied a detailed critique of the mathematical proposals of Cassuto, Young, and several other commentators. [28]

2. Statistical theory provides evidence against fabrication

Having carried out a detailed technical analysis of the biblical longevities, Walter Makous found that they show “no reliable deviations from statistical independence” and that they exhibit “reliable differences from the properties of fabricated numbers.” He concluded that “there is no evidence that these numbers are artificial” and that “the mathematical properties of these numbers favor natural origin.” [29] Donald A. Huebner attempted briefly to dispute Makous’s work [30], but Makous appears to have adequately addressed Huebner’s objections [31].

3. The Genesis numbers need not be “random” since God is in control of them

Some commentators (e.g., Hill [32] and Sparks [33]) have stated or implied that the patriarchal numbers in Genesis ought to fit a “random” pattern. But this expectation is unwarranted given that Genesis presents a sovereign God who is fully in control of the timing of human events, including birth and death.

Passages exhibiting God’s control over the timing of birth include:

• Genesis 4:1 — At the time of Cain’s birth, Eve acknowledges of “the help of the Lord.”
• Genesis 17:15-19; 18:10-14; 21:1-5 — God foretells the birth of Isaac, and then fulfills his promise when Abraham is 100 years old. (Note that this nice round, potentially “symbolic” number is in fact exact since, according to Genesis 17:1,24, Abraham’s age had been 99 the year before. Incidentally, Abraham and Sarah’s ages receive significant mention in the New Testament, in contexts discussing their faith in God’s word, which is exemplary for us: Romans 4:19; Hebrews 11:11f.)
• Genesis 25:21 — Isaac’s fathering of Jacob and Esau is said to have been the result of the Lord answering his prayer.
• Genesis 29:31-33; 30:2,17-20,22-24 — The births of several of Jacob’s children are stated to have been the result of divine intervention (God “opened” Leah’s womb, “listened” to Leah, and “remembered” Rachel).

Texts indicating God’s sovereignty over the timing of death include:

• Genesis 5:23f. — Enoch’s time on earth, 365 years, was finished when “God took him.” Though Enoch did not actually die (Hebrews 11:5), it was God’s direct action that brought his earthly life to a close.
• Genesis 6:3 — The Lord pronounces that man’s “days shall be 120 years.” Whether this refers to the period of time until the flood would come, or to the shortened human longevity that would take effect in due course, it is an allusion to God’s control over the timing of human death.
• Genesis 6:7,13,17; 7:4,23 — The flood, which ended all human lives but eight, was specifically timed by God.

Conclusion

This article offers a new argument, a reductio ad absurdum, that will complement other defenses of the validity of the age numbers in Genesis 5 and 11. The argument from statistical improbability, as presented by Hill (and Sparks), was found to apply just as strongly to the monarchal lifespans as to the patriarchal ages at death. A variety of intriguing mathematical patterns was observed among the monarchal numbers, including connections involving repetition and addition/subtraction; between-age differences; Mesopotamian-style formulations; Babylonian algebraic expressions; six-member chiasms; “triple 4” and “triple 7” features; and an almost perfect pattern in the age rankings. Taken together, this evidence would seem to provide justification for suspicion that the monarchal age numbers have been contrived. If such patterns had been detected among the patriarchal ages, scholars would undoubtedly blazon them as evidence of contrivance. To my knowledge, however, no one actually disputes the historicity of the ten monarchs and their longevities (nor do I myself). By the same logic, then, I urge that no one should dismiss the reality of the patriarchal ages based simply on allegations of statistical improbability or the various mathematical patterns that can, with ingenuity, be “discovered.”

Inveterate seekers of patterns are we:
Inspecting, detecting, until we can see
The picture unfold as we’d like it to be!

References / Notes

1. Duane L. Christensen, “Did People Live to Be Hundreds of Years Old Before the Flood? No,” in The Genesis Debate: Persistent Questions about Creation and the Flood, ed. Ronald Youngblood (Grand Rapids, MI: Baker Book House, 1990), 167.

2. Carol A. Hill, “Making Sense of the Numbers of Genesis,” Perspectives on Science and Christian Faith, 55, no. 4 (2003): 245. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

3. Ibid., 245. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

4. Umberto Cassuto, A Commentary on the Book of Genesis, Part I, From Adam to Noah, Genesis I – VI 8, trans. Israel Abrahams (Jerusalem: The Magnes Press, The Hebrew University, 1961 [original 1944]), 252-265, 276-290; ____, A Commentary on the Book of Genesis, Part II, From Noah to Abraham, Genesis VI 9 – XI 32, trans. Israel Abrahams (Jerusalem: The Magnes Press, The Hebrew University, 1964 [original 1949]), 256-266.

5. C. A. Hill, “Making Sense of the Numbers of Genesis,” 249. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

6. Ibid., 239. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

7. Carol A. Hill, “Response to P. G. Nelson’s ‘Numerology in Genesis’,” Perspectives on Science and Christian Faith, 60, no. 2 (2008): 144. http://www.asa3.org/ASA/PSCF/2008/PSCF6-08Hill2.pdf.

8. Donald V. Etz, “The Numbers of Genesis V 3-31: A Suggested Conversion and Its Implications,” Vetus Testamentum, 43, no. 2 (1993): 182.

9. Dwight Wayne Young, “The Influence of Babylonian Algebra on Longevity Among the Antediluvians,” Zeitschrift für die Alttestamentliche Wissenschaft, 102, no. 3 (1990): 334.

10. Kenton L. Sparks, “Genesis 1–11 as Ancient Historiography,” in Genesis: History, Fiction, or Neither? Three Views on the Bible’s Earliest Chapters, ed. Charles Halton (Grand Rapids, MI: Zondervan, 2015), 120.

11. D. W. Young, “The Influence of Babylonian Algebra on Longevity Among the Antediluvians,” 334.

12. D. V. Etz, “The Numbers of Genesis V 3-31: A Suggested Conversion and Its Implications,” 176, 182.

13. I have been accused of “cherry-picking” in my selecting of these particular monarchs. Here’s how it happened. When I began to look for possible patterns among historical figures, I first considered the lists of Canadian prime ministers and U.S. presidents, but rejected both for lack of perceived mathematical patterns. The British monarchs were my next choice. It therefore took me only three tries before I located such a wonderful pattern-laden list! Furthermore, this was the very first genealogy-based list that I examined.

14.Wikipedia. “Anne, Queen of Great Britain,” https://en.wikipedia.org/wiki/Anne,_Queen_of_Great_Britain. Anne reigned from 1702 to 1714. Only after the union of Scotland with England to form “Great Britain” in 1707 was she known as a “British” monarch, according to Wikipedia’s use of the term “British.” When Anne died, over 50 of her relatives were more closely related to her than was George I. But since all of those were Roman Catholic, they were prohibited by law from acceding to the throne. Wikipedia. “George I of Great Britain,” https://en.wikipedia.org/wiki/George_I_of_Great_Britain.

15. Genesis 5:1-32; 9:28f.; Wikipedia. “List of British monarchs,” https://en.wikipedia.org/wiki/List_of_British_monarchs.

16. C. A. Hill, “Making Sense of the Numbers of Genesis,” 245. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

17. Ibid., 245. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

18. The first six monarchs, up to and including Victoria, belonged to the House of Hanover. Edward VII, though a son of Victoria, was assigned to his father’s designation, the House of Saxe-Coburg and Gotha. The last three kings (and the present queen, Elizabeth II) are placed within the House of Windsor, but this new name is unrelated to genealogy: the previous House name was changed during the First World War simply because it sounded too German. Wikipedia. “House of Windsor,” https://en.wikipedia.org/wiki/House_of_Windsor.

19. C. A. Hill, “Making Sense of the Numbers of Genesis,” 245. http://www.asa3.org/ASA/PSCF/2003/PSCF12-03Hill.pdf.

20. P. G. Nelson, “Numerology in Genesis,” Perspectives on Science and Christian Faith, 60, no. 1 (2008), 70-71. http://www.asa3.org/ASA/PSCF/2008/PSCF3-08Nelson.pdf.

21. C.A. Hill, “Response to P. G. Nelson’s ‘Numerology in Genesis’,” 144. http://www.asa3.org/ASA/PSCF/2008/PSCF6-08Hill2.pdf.

22. U. Cassuto, A Commentary on the Book of Genesis, Part II, 256-257.

23. Dwight Wayne Young, “On the Application of Numbers from Babylonian Mathematics to Biblical Life Spans and Epochs,” Zeitschrift für die Alttestamentliche Wissenschaft, 100, no. 3 (1988): 343

24. Ibid., 340f.

25. U. Cassuto, A Commentary on the Book of Genesis, Part II, 258.

26. Dwight Wayne Young, “On the Application of Numbers from Babylonian Mathematics to Biblical Life Spans and Epochs,” 331.

27. D. V. Etz, “The Numbers of Genesis V 3-31: A Suggested Conversion and Its Implications,” 177.

28. Richard Johnson, “The Genealogies of Genesis: A Study of Their Structure and Function” (MA dissertation, London Bible College, 1989), 36-43. To request a pdf copy of this work, contact Richard Johnson at richard@qohelethresources.co.uk.

29. Walter Makous, “Biblical Longevities: Empirical Data or Fabricated Numbers?” Perspectives on Science and Christian Faith, 63, no. 2 (2011): 117, 123, 129. http://www.asa3online.org/asa3.org/ASA/PSCF/2011/PSCF6-11Makous.pdf.

30. Donald A. Huebner, “Biblical Longevities: Some Questions and Issues,” Perspectives on Science and Christian Faith, 63, no. 4 (2011): 287f. http://www.asa3.org/ASA/PSCF/2011/PSCF12-11Huebner.pdf.

31. Walter Makous, “Biblical Longevities: Reply to Huebner,” Perspectives on Science and Christian Faith, 64, no. 2 (2012): 143. http://www.asa3.org/ASA/PSCF/2012/PSCF6-12Makous.pdf.

32. C. A. Hill, “Response to P. G. Nelson’s ‘Numerology in Genesis’,” 144. http://www.asa3.org/ASA/PSCF/2008/PSCF6-08Hill2.pdf.

33. K. L. Sparks, “Genesis 1–11 as Ancient Historiography,” 120.